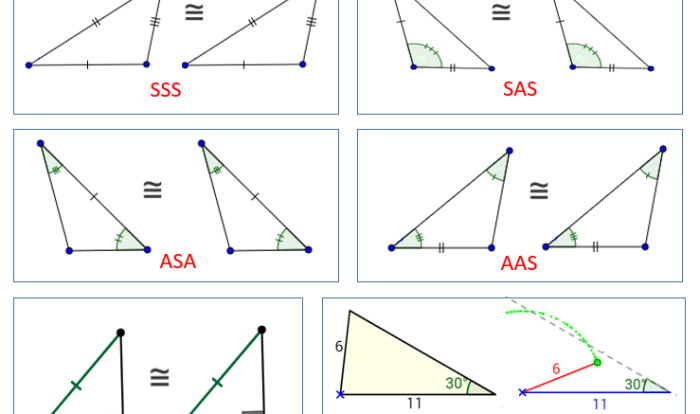
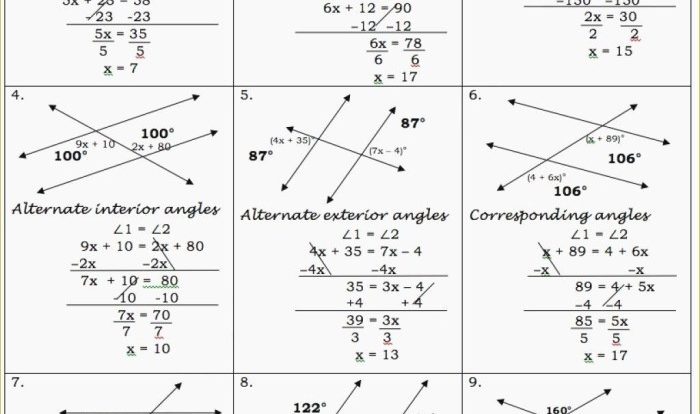
Geometry chapter 3 parallel and perpendicular lines answer key – Prepare to delve into the fascinating world of geometry as we unlock the secrets of parallel and perpendicular lines in Chapter 3. This comprehensive answer key will guide you through the intricacies of these fundamental concepts, providing clarity and empowering you to conquer any geometry challenge that comes your way.
Embark on a journey of discovery as we explore the defining characteristics of parallel and perpendicular lines, unravel the mysteries of their slopes, and uncover the hidden relationships that govern their interactions. Real-world examples will illuminate the practical applications of these concepts, bringing geometry to life before your very eyes.
Understanding Parallel and Perpendicular Lines
In geometry, parallel and perpendicular lines are fundamental concepts that play a crucial role in understanding various geometric relationships and solving geometric problems. Understanding these lines’ properties and relationships is essential for students of geometry and those working in fields that involve geometry.
Definition of Parallel and Perpendicular Lines
Parallel lines are lines that lie in the same plane and never intersect. Perpendicular lines, on the other hand, are lines that intersect at right angles (90 degrees).
Slope of Parallel and Perpendicular Lines
The slope of a line is a measure of its steepness. Parallel lines have the same slope, while perpendicular lines have slopes that are negative reciprocals of each other.
Examples of Parallel and Perpendicular Lines
Examples of parallel lines can be found in everyday life, such as the sides of a rectangle or the rungs of a ladder. Perpendicular lines are also common, such as the edges of a cube or the spokes of a wheel.
Properties of Parallel and Perpendicular Lines

Properties of Parallel Lines
- Equidistant: Parallel lines are always the same distance apart.
- No Points of Intersection: Parallel lines never intersect.
Properties of Perpendicular Lines
- Right Angles: Perpendicular lines intersect at right angles (90 degrees).
- Perpendicular Bisectors: A perpendicular line that intersects a line segment at its midpoint is called a perpendicular bisector.
Geometric Diagrams
Geometric diagrams can be used to demonstrate the properties of parallel and perpendicular lines. For example, a diagram of parallel lines shows that they are always the same distance apart, while a diagram of perpendicular lines shows that they intersect at right angles.
Theorems Related to Parallel and Perpendicular Lines

Parallel Line Theorem
If a transversal intersects two parallel lines, then the alternate interior angles are congruent.
Alternate Interior Angles Theorem and its Converse, Geometry chapter 3 parallel and perpendicular lines answer key
If a transversal intersects two lines and the alternate interior angles are congruent, then the lines are parallel.
Same-Side Interior Angles Theorem and its Converse
If a transversal intersects two lines and the same-side interior angles are supplementary (add up to 180 degrees), then the lines are parallel.
Applications of Parallel and Perpendicular Lines
Applications in Architecture, Engineering, and Design
Parallel lines are used in architecture to create straight lines and sharp angles, while perpendicular lines are used to create right angles and perpendicular walls. In engineering, parallel lines are used to create stable structures, while perpendicular lines are used to create joints and supports.
Applications in Construction, Surveying, and Navigation
Perpendicular lines are used in construction to create square corners and level surfaces. In surveying, perpendicular lines are used to establish property boundaries and measure distances. In navigation, perpendicular lines are used to determine the direction of travel.
Solving Problems Involving Parallel and Perpendicular Lines

Table of Key Concepts
| Concept | Definition |
|---|---|
| Parallel lines | Lines that lie in the same plane and never intersect. |
| Perpendicular lines | Lines that intersect at right angles (90 degrees). |
| Slope | A measure of the steepness of a line. |
| Parallel Line Theorem | If a transversal intersects two parallel lines, then the alternate interior angles are congruent. |
| Alternate Interior Angles Theorem | If a transversal intersects two lines and the alternate interior angles are congruent, then the lines are parallel. |
| Same-Side Interior Angles Theorem | If a transversal intersects two lines and the same-side interior angles are supplementary (add up to 180 degrees), then the lines are parallel. |
Flowchart for Solving Problems
- Identify the given information.
- Determine which theorem or property to use.
- Apply the theorem or property to solve the problem.
- Check your answer.
Practice Problems
1. Prove that the lines y = 2x + 1 and y = -x + 3 are perpendicular.
2. Find the equation of the line that is parallel to y = 3x – 2 and passes through the point (2, 5).
Q&A: Geometry Chapter 3 Parallel And Perpendicular Lines Answer Key
What is the difference between parallel and perpendicular lines?
Parallel lines never intersect, while perpendicular lines intersect at right angles (90 degrees).
How can I identify parallel and perpendicular lines in a diagram?
Parallel lines have the same slope, while perpendicular lines have slopes that are negative reciprocals of each other.
What are some real-world applications of parallel and perpendicular lines?
Parallel lines are used in architecture to create structures that are stable and visually appealing. Perpendicular lines are used in construction to ensure that walls are straight and perpendicular to the ground.