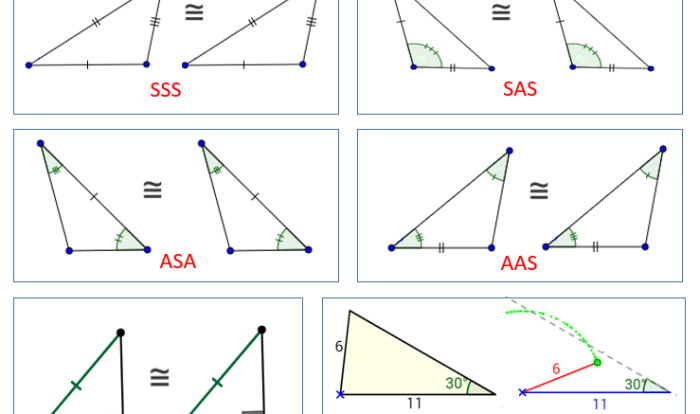
Parallel lines cut by a transversal activity presents a captivating exploration of the geometric properties and applications of parallel lines intersected by a transversal. Delving into the fundamental concepts of parallel lines and transversals, this discussion unravels the intriguing relationships that govern these geometric elements.

When a transversal intersects two or more parallel lines, it creates a series of angles that exhibit specific properties. These properties, including corresponding angles, alternate interior angles, and same-side interior angles, provide a foundation for understanding the behavior of parallel lines in various geometric constructions and real-world applications.

Parallel Lines Cut by a Transversal

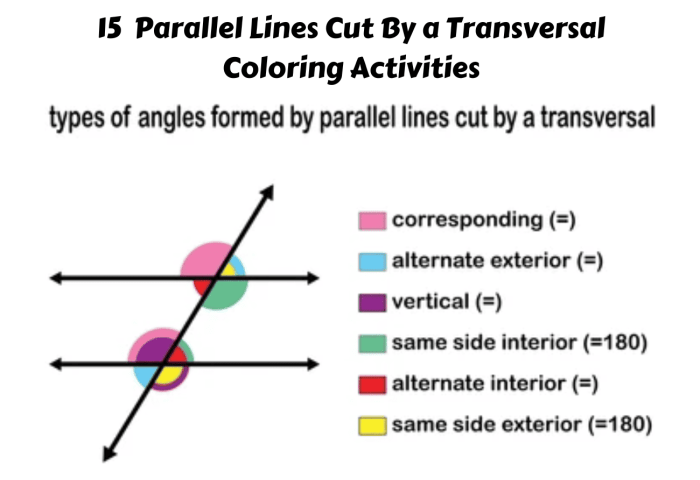
Parallel lines are lines that never intersect. A transversal is a line that intersects two or more parallel lines. When a transversal intersects two parallel lines, it creates eight angles. These angles are classified into four types: corresponding angles, alternate interior angles, same-side interior angles, and exterior angles.

Properties of Parallel Lines Cut by a Transversal

Corresponding Angles

Corresponding angles are angles that are in the same position relative to the transversal. Corresponding angles are congruent, meaning they have the same measure.

Alternate Interior Angles

Alternate interior angles are angles that are on opposite sides of the transversal and inside the parallel lines. Alternate interior angles are congruent.

Same-Side Interior Angles, Parallel lines cut by a transversal activity

Same-side interior angles are angles that are on the same side of the transversal and inside the parallel lines. Same-side interior angles are supplementary, meaning they add up to 180 degrees.

Applications of Parallel Lines Cut by a Transversal

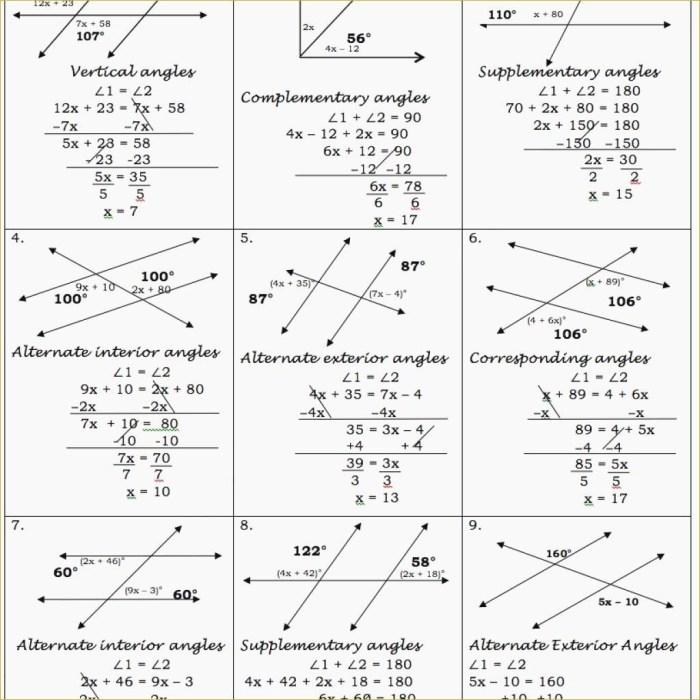
Parallel lines cut by a transversal have many applications in geometry. These applications include:

• Finding the measure of unknown angles
• Constructing parallel lines
• Solving geometry problems

Geometric Constructions Involving Parallel Lines and Transversals: Parallel Lines Cut By A Transversal Activity

Parallel lines cut by a transversal can be used to construct parallel lines and perpendicular lines. To construct parallel lines, draw a transversal and mark the corresponding angles. Then, draw lines parallel to the transversal through the points where the transversal intersects the parallel lines.

To construct perpendicular lines, draw a transversal and mark the alternate interior angles. Then, draw lines perpendicular to the transversal through the points where the transversal intersects the parallel lines.

Real-World Examples of Parallel Lines Cut by a Transversals

Parallel lines cut by a transversal can be found in many real-world applications, such as:

• Railroad tracks
• Bridges
• Buildings

FAQ Compilation

What are parallel lines?

Parallel lines are lines that lie in the same plane and never intersect, no matter how far they are extended.

What is a transversal?

A transversal is a line that intersects two or more other lines at distinct points.

What are corresponding angles?

Corresponding angles are angles that are located in the same relative positions on different lines.