Delving into the realm of geometry, we embark on an exploration of parallelograms, unlocking their properties and unraveling the methods to prove their existence. Join us as we delve into the fascinating world of prove ABCD is a parallelogram, where clarity and precision intertwine to illuminate the path of mathematical discovery.
In this comprehensive guide, we will provide a clear and concise definition of a parallelogram, examining its key characteristics that set it apart from other quadrilaterals. We will then embark on a journey through the various properties that define parallelograms, exploring their implications and uncovering their practical applications.
Definition of a Parallelogram
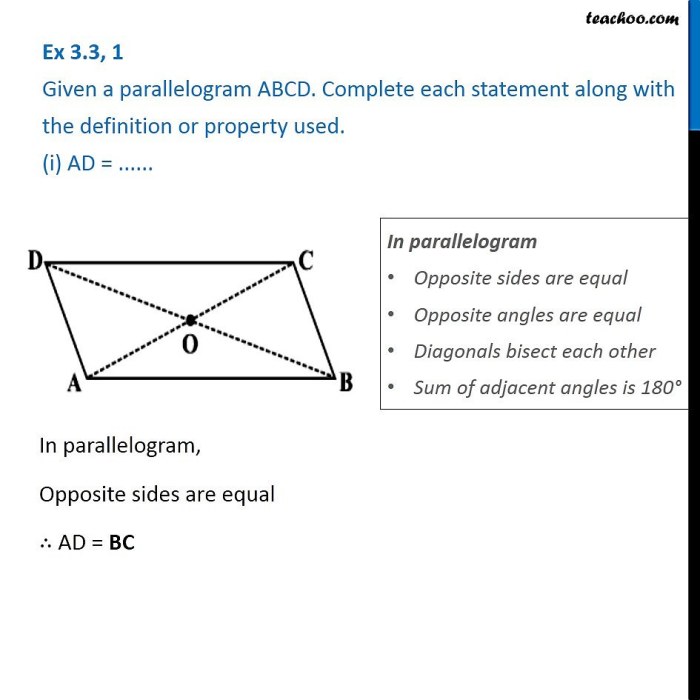
A parallelogram is a two-dimensional geometric figure with four sides and four angles. It is a special type of quadrilateral, which means it has four straight sides. Parallelograms are characterized by their opposite sides being parallel and equal in length.
Key Characteristics of a Parallelogram
- Opposite sides are parallel and equal in length.
- Opposite angles are equal in measure.
- Diagonals bisect each other (divide each other into two equal parts).
Properties of a Parallelogram: Prove Abcd Is A Parallelogram
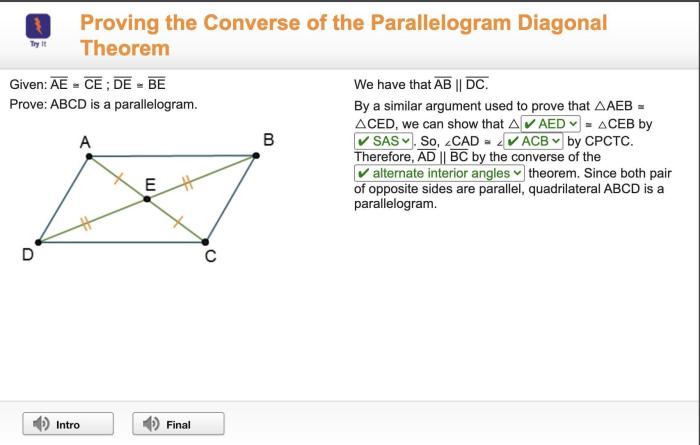
Parallelograms possess several unique properties that distinguish them from other quadrilaterals. These properties provide valuable insights into the behavior and characteristics of parallelograms, making them useful in various mathematical applications.
Opposite Sides are Parallel and Congruent
In a parallelogram, the opposite sides are always parallel and congruent. This means that the two pairs of opposite sides have the same length and run in the same direction. For example, in the parallelogram ABCD, side AB is parallel and congruent to side CD, and side BC is parallel and congruent to side AD.
Opposite Angles are Congruent
Another property of parallelograms is that the opposite angles are congruent. This means that the two pairs of opposite angles have the same measure. For example, in parallelogram ABCD, angle A is congruent to angle C, and angle B is congruent to angle D.
Diagonals Bisect Each Other, Prove abcd is a parallelogram
The diagonals of a parallelogram bisect each other. This means that the point where the diagonals intersect divides each diagonal into two equal parts. For example, in parallelogram ABCD, the diagonals AC and BD intersect at point O, and AO = OC and BO = OD.
Area Formula
The area of a parallelogram can be calculated using the formula: Area = base × height. The base is the length of one of the parallel sides, and the height is the perpendicular distance between the parallel sides.
Applications of Parallelogram Properties
The properties of parallelograms find applications in various fields, including architecture, engineering, and design. For example, the fact that opposite sides are parallel and congruent is used in the design of bridges and buildings to ensure structural stability. The property of opposite angles being congruent is used in the creation of patterns and tessellations in art and design.
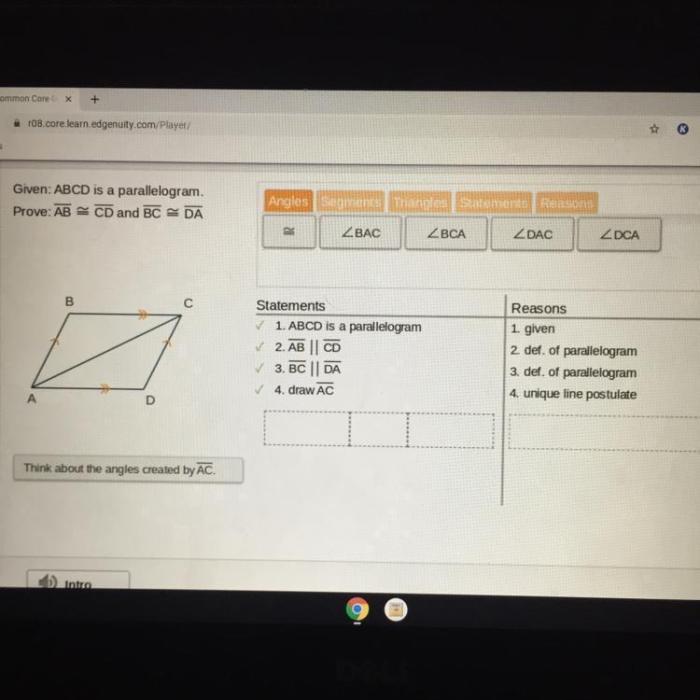
Methods to Prove a Quadrilateral is a Parallelogram
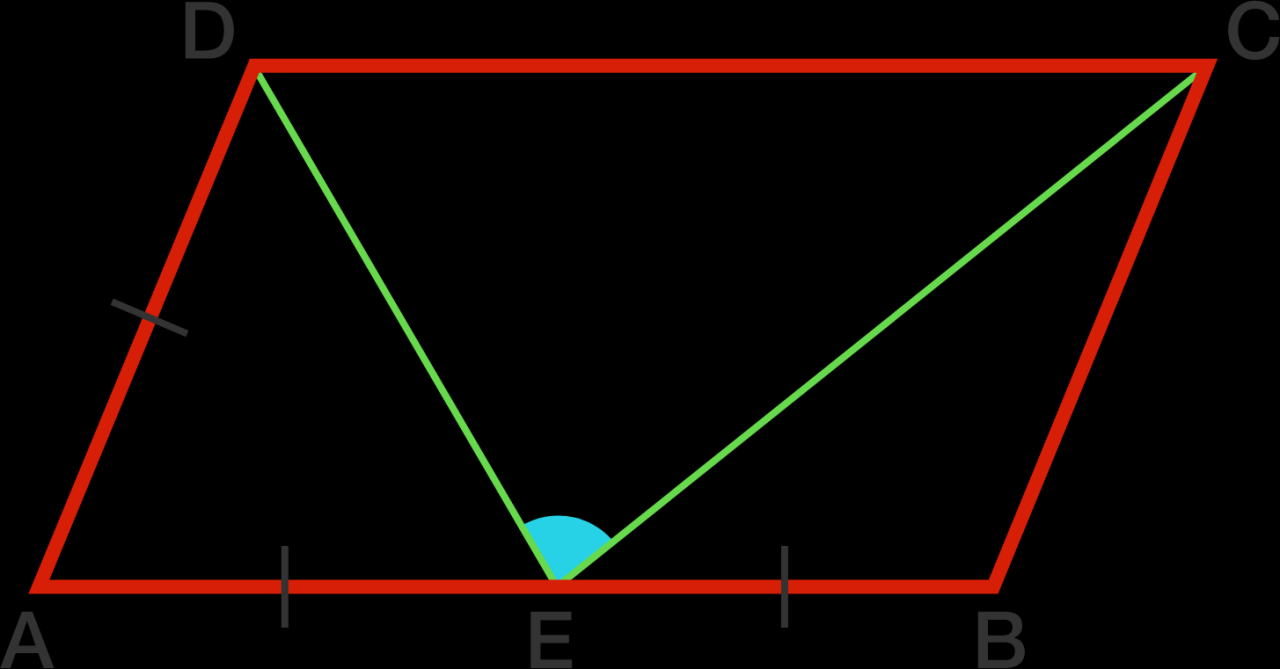
There are several methods that can be used to prove that a quadrilateral is a parallelogram. These methods are based on the properties of parallelograms, which include having opposite sides parallel and equal in length, and having opposite angles equal.
Method 1: Opposite Sides Parallel and Equal in Length
- Show that the opposite sides of the quadrilateral are parallel. This can be done by showing that the slopes of the opposite sides are equal.
- Show that the opposite sides of the quadrilateral are equal in length. This can be done by using the distance formula to calculate the lengths of the sides.
Method 2: Opposite Angles Equal
- Show that the opposite angles of the quadrilateral are equal. This can be done by using the angle addition postulate to show that the sum of the angles in each pair of opposite angles is 180 degrees.
Method 3: Diagonals Bisect Each Other
- Show that the diagonals of the quadrilateral bisect each other. This can be done by showing that the point of intersection of the diagonals divides each diagonal into two equal segments.
Geometric Constructions

Geometric constructions are useful tools for proving that a quadrilateral is a parallelogram. By constructing specific lines and angles, we can demonstrate the properties of a parallelogram and conclude that the quadrilateral in question satisfies those properties.
Drawing Parallels
To construct a line parallel to a given line, we can use a straightedge and a compass. Place the straightedge along the given line and use the compass to mark two points on the line. Then, place the compass at one of the marked points and draw an arc that intersects the given line.
Without changing the compass setting, place the compass at the other marked point and draw another arc that intersects the given line. The line connecting the two intersection points will be parallel to the given line.
Constructing Perpendicular Bisectors
To construct the perpendicular bisector of a line segment, we can use a compass and a straightedge. Place the compass at one endpoint of the line segment and draw an arc that intersects the line segment. Without changing the compass setting, place the compass at the other endpoint and draw another arc that intersects the line segment.
In geometry, proving that a quadrilateral is a parallelogram involves demonstrating that its opposite sides are parallel. To learn more about geometric proofs, check out the resources for a segment of a radio show . These resources provide clear explanations and examples to help you understand the concepts involved in proving that abcd is a parallelogram.
The line connecting the two intersection points will be the perpendicular bisector of the line segment.
Applications of Proving a Quadrilateral is a Parallelogram
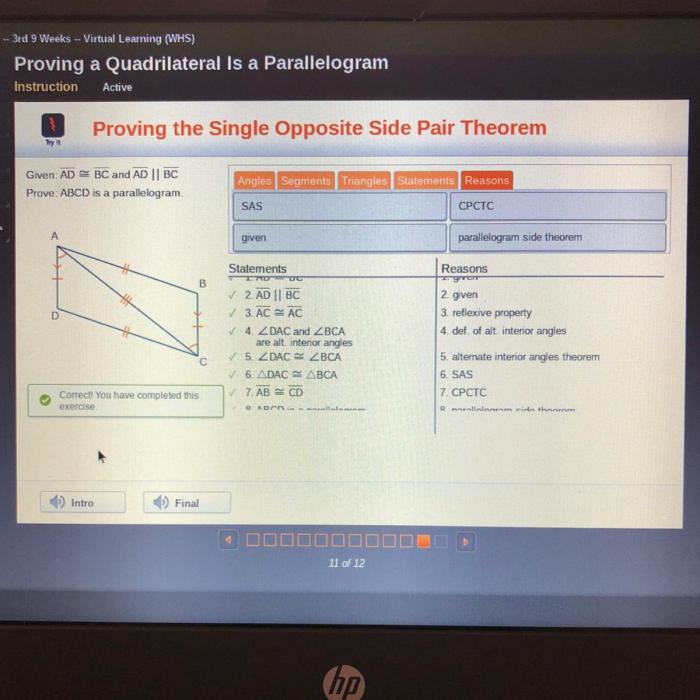
Proving that a quadrilateral is a parallelogram is a valuable skill with numerous practical applications. It enables individuals to solve geometry problems accurately and make informed decisions in real-world situations.
Examples of Practical Applications
- Construction and Architecture:Parallelograms are commonly used in construction and architecture due to their structural stability and aesthetic appeal. Proving that a quadrilateral is a parallelogram ensures the accuracy and integrity of building designs.
- Engineering and Design:Parallelograms are employed in various engineering and design applications, such as bridge construction and vehicle suspension systems. Proving that a quadrilateral is a parallelogram allows engineers to calculate forces, stresses, and other parameters accurately.
- Art and Graphic Design:Parallelograms are often used as design elements in art and graphic design. Proving that a quadrilateral is a parallelogram enables artists and designers to create precise and visually appealing compositions.
FAQ Summary
What is the definition of a parallelogram?
A parallelogram is a quadrilateral with opposite sides parallel and of equal length.
What are the key properties of a parallelogram?
Opposite sides are parallel and equal in length, opposite angles are equal, and diagonals bisect each other.
How can I prove that a quadrilateral is a parallelogram?
There are several methods, including proving that opposite sides are parallel and equal, or that diagonals bisect each other.